深度学习常见模型-CNN

CNN的来源

CNN由纽约大学的Yann LeCun于1989年提出。CNN本质上是一个多层感知机，其成功的原因关键在于它所采用的局部连接和共享权值的方式。

一方面减少了的权值的数量使得网络易于优化，另一方面降低了过拟合的风险。CNN是神经网络中的一种，它的权值共享网络结构使之更类似于生物神经网络，降低了网络模型的复杂度，减少了权值的数量。

权重共享：在卷积神经网络中，卷积层的每一个卷积滤波器重复的作用于整个感受野中，对输入图像进行卷积，卷积结果构成了输入图像的特征图，提取出图像的局部特征。每一个卷积滤波器共享相同的参数，包括相同的权重矩阵和偏置项。共享权重的好处是在对图像进行特征提取时不用考虑局部特征的位置。而且权重共享提供了一种有效的方式，使要学习的卷积神经网络模型参数数量大大降低。

CNN的网络架构

卷积神经网络结构包括：卷积层，降采样层，全链接层。每一层有多个特征图，每个特征图通过一种卷积滤波器提取输入的一种特征，每个特征图有多个神经元。

卷积层（Conv）

这一层就是卷积神经网络最重要的一个层次，也是“卷积神经网络”名字来源。
在卷积层中，有两个关键操作：局部关联和窗口滑动。局部关联将每个神经元看作一个滤波器（filter），窗口滑动则使filter对局部数据进行计算。
除了这两个操作外，还有两个名词：步长和填充值。步长（stride）为窗口一次滑动的长度，而填充值请看下图的例子。比如有一个5x5像素大小的图片，步长取2，那么则有一个像素没有办法获取到，那应该怎么办呢？

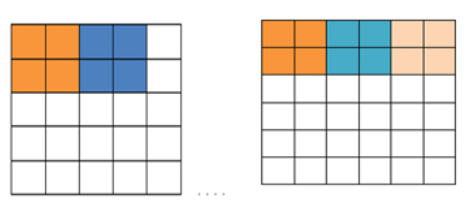
再举一个例子，图片中输入的是一个3x4的矩阵，卷积核是一个2x2的矩阵。我们假设卷积是一次移动一个像素来操作的，那么我们首先对左上角2x2局部矩阵与卷积核进行卷积操作，即各个位置的元素相乘再相加，得到的输出矩阵S的S₀₀的元素值为aw+bx+ey+fz。然后我们将卷积核向右平移一个像素，现在是（b,c,f,g）四个元素构成的矩阵和卷积核来卷进，得到了输出矩阵S的S₀₁的元素，以此类推，可以得到矩阵S的S₀₂，S₁₀，S₁₁，S₁₂的元素，具体过程如下图所示。

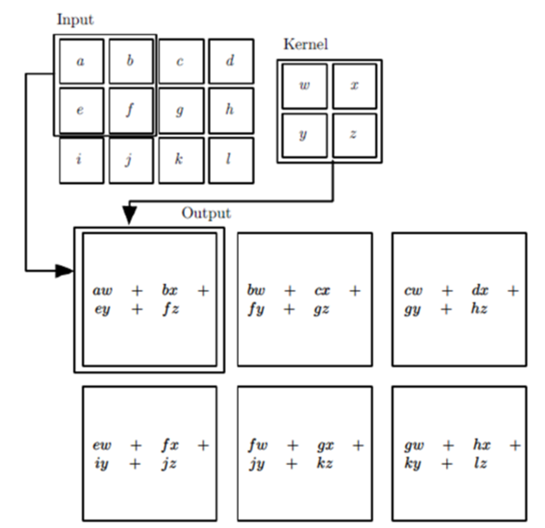
再举一个卷积过程的例子如下：我们有下面这个绿色的5x5输入矩阵，卷积核是一个下面这个黄色的3*3矩阵。卷积的步幅是一个像素。则卷积的过程如下面的动图。卷积的结果是一个3x3的矩阵。

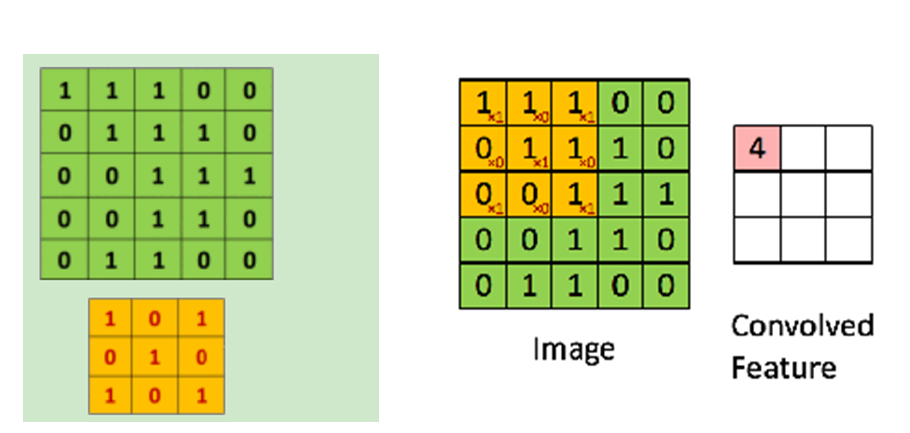
上面举的例子都是二维的输入，卷积的过程比较简单，那么如果输入是多维的呢？比如在前面一组卷积层+池化层的输出是3个矩阵，这3个矩阵作为输入呢，那么我们怎么去卷积呢？又比如输入的是对应RGB的彩色图像，即是三个分布对应R，G和B的矩阵呢？

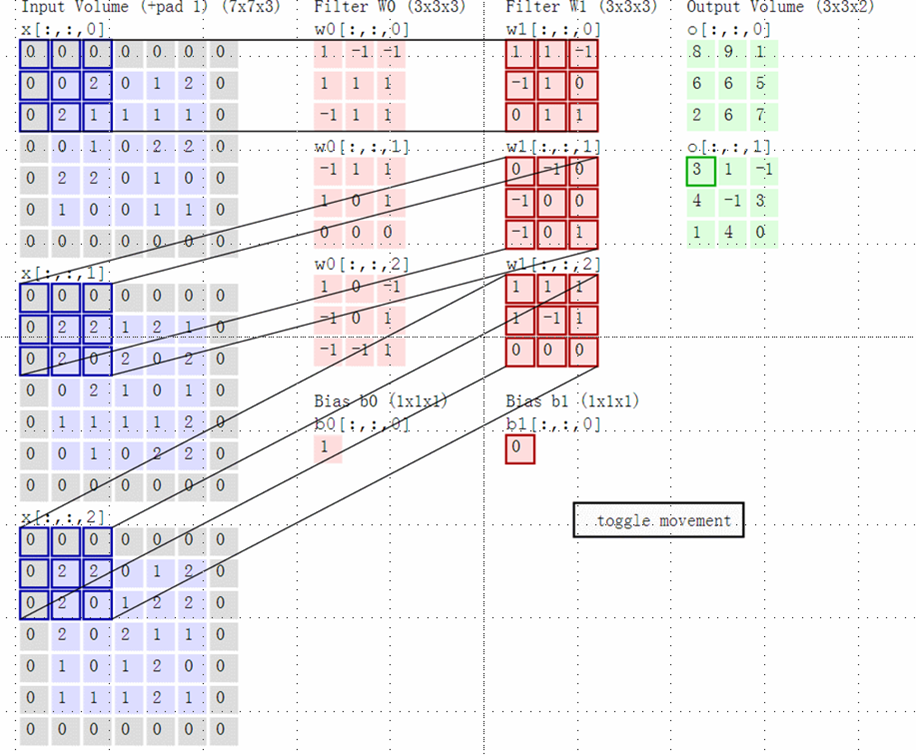
这里实际输入的是3个5x5的矩阵，在原来输入的周围加上值为0的一层padding，则输入变为如图所示的7x7的矩阵。例子里面使用了两个卷积核，我们先关注与卷积核W₀。由于输入的是3个7x7的矩阵，也可以说成7x7x3的张量，所以我们对应的卷积核W₀的最后一个参数也必须是3的张量，这里卷积核W₀的单独子矩阵维度为3x3.那么卷积核W₀实际为一个3x3x3的张量。同时和上面的例子不同的是，这里的步长为2，即每次卷积后卷积核会向后移动2个像素的位置。
蓝色矩阵（输入图像） 对 粉丝矩阵（filter） 进行矩阵内积计算并将三个内积运算的结果与偏移量b像加，比如上图中，3+0+0+0=3，计算后的值，即绿色矩阵 中的一个元素。

池化层（Pooling）

池化层，又称为降采样层，使用的原因为：根据图像局部相关性的原理，对图像进行子采样可能减少计算量，同时保持图像的旋转不变性。相比卷积层的复杂，池化层简单的多，所谓的池化，个人理解就是对输入张量的各个子矩阵进行压缩。假如是2x2的池化滤波，那么就将子矩阵的每个2x2个元素变为一个元素；如果为3x3的池化滤波，就将子矩阵每3x3个元素变成一个元素，这样输入矩阵的维度就变小了。
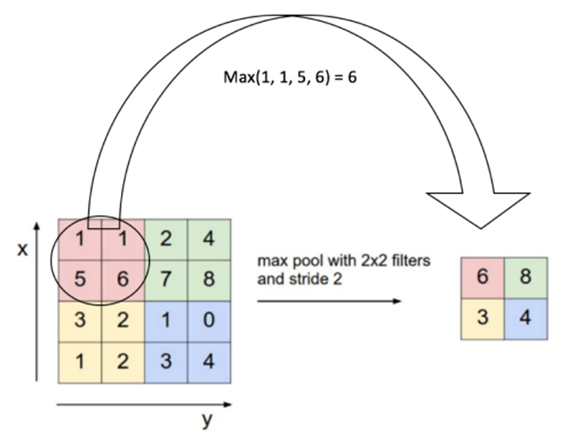
如果想将矩阵中每NxN个元素变成一个元素，则需要一个共同的池化标准。常见的池化标准有2个：MAX和Average。即取对应区域的最大值或者平均值作为池化后的元素值。下图的例子中采用的是最大池化方法，2x2的池化滤波，步长为2.首先对红色2x2区域进行池化，此区域中最大值对6，则对应池化输出的值为6。然后滤波进行移动，由于步长为2，则移动至图中绿色区域，输出最大值为8，以此类推，最终，输入的4x4的矩阵经过池化过程后，变为2x2的矩阵，得到了压缩。

全连接层（Full Connecting）

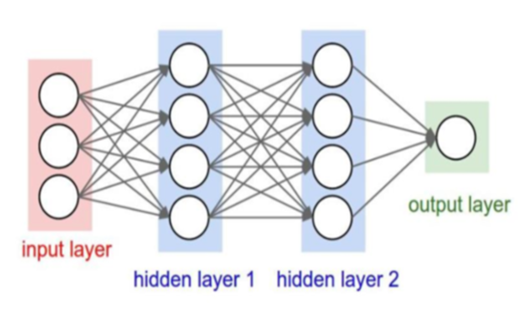
每层之间的神经元都有权重连接，通常全连接层在卷积神经网络的尾部，是同传统神经网络神经元的连接方式是一样的。全连接层和卷积层比较相似，但全连接层的输出是一个Nx1大小的向量，并通过几个全连接层对向量进行将为操作，一般采用softmax全连接。

总结

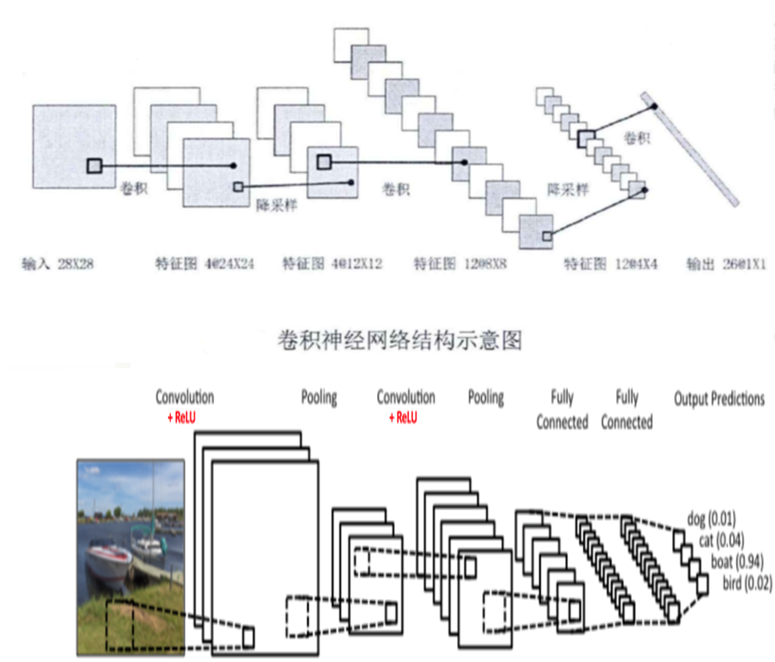
一般CNN的结构依次为

1. input
2. ((conv –> relu) x N–>pool?) x M
3. (fc –> relu) x K
4. fc

卷积神经网络的训练算法

• 与一般的机器学习算法相比，先定义Loss function,衡量和实际结果之间的差距；
• 找到最小化损失函数的W（权重）和b（偏置），CNN里面最常见的算法为SGD（随机梯度下降）。

卷积神经网络的优缺点

优点

• 共享卷积核，便于处理高维数据；
• 不像机器学习人为提取特征，网络训练权重自动提取特征，且分类效果好。

缺点

• 需要大量训练样本和好的硬件支持（GPU、TPU…）;

• 物理含义模糊（神经网络是一种难以解释的“黑箱模型”，我们并不知道卷积层到底提取的是什么特征）。

卷积神经网络的典型结构

• LeNet,最早用于手写体数字识别的卷积神经网络。
• AlexNet，2012年ILSVRC比赛中获得第一名，远超过第二名，比LeNet更深，用多层小卷积层进行叠加替换大卷积层。
• ZFNet，2013年ILSVRC比赛冠军
• GoogleNet，2014年ILSVRC比赛冠军
• VGGNet，2014年ILSVRC比赛中的模型，图像识别上略差于GoogleNet，但是在很多图像转化学习问题（比如object detection）上效果很好。

实战演练

猫狗大战，即一个简单的二分类问题，训练出一个自动判别猫狗的模型

训练集（共25000张图片，猫狗各12500张）
测试集（共3000张图片，猫狗各1500张）

我们通过Tensorflow这个深度学习框架来构建我们的分类网络。通过其自带的可视化工具Tensorboard我们可以看到网络的详细结构，如下左图所示。
模型训练完成后，我们用测试集来测试模型的泛化能力，输入一张测试图片，导入模型，输出分类结果，示例见下右图。